MIDTERM REVIEW SHEET

LISTS: Most basic & versatile. Sequential container; programmer controls the order items appear.

SET: Like a list, but only unique items can exist. The computer controls the order of items. Can be ordered or unordered.

QUEUE: First in first out. Items enter the back and are popped off the front. Use .push(o) to add o to end. Use pop() to remove the object that is at the front of the queue. Faster than list/vector. Things like print jobs.

MAPS: Similar to dictionary in Python. Unique object : other object.

STACKS: Last in first out. Good for things that need to be reversed. isEmpty, push(o), pop(), and top() are all methods.

PRIORITY QUEUE: Like queues, but you can insert things in a specific order. top() instead of front() for highest priority item.

BINARY SEARCH Big(o): worst/average = O(log n); best = O(1)

Algorithm	Best Case	Worst Case
Bubble Sort	$O (n)$	$O (n^{2})$
Selection Sort	$O (n^{2})$	$O (n^{2})$
Insertion Sort	$O (n)$	$O (n^{2})$
Merge Sort	$O (n \log n)$	$O (n \log n)$
Quick Sort	$O (n \log n)$	$O (n^{2})$


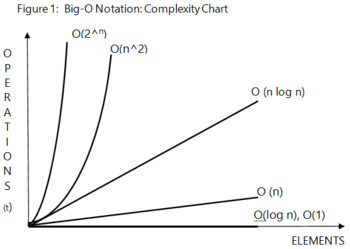BUBBLE SORT
do:
for each pair of adjacent elements:

if the values are out of order:
swap the values
while the array is not sorted

Look at each adjacent pair in the array
Swap adjacent pairs if they are out of order
Repeat until no swaps are made

worst-case runtime of bubble sort $O (n^{2})$ . Each pass of the array is $O (n)$ , and up to $n$ passes may be required. Multiply that together to get $O (n^{2}) .$

INSERTION SORT

FOR EACH i FROM 1 TO size - 1
    SET j TO i
    SET item TO list[j]
    WHILE j > 0 AND list[j - 1] > item
        SET list[j] TO list[j - 1]
        DECREMENT j BY 1
    END WHILE
    SET list[j] TO item
END FOR

The worst-case runtime is $O (n^{2})$ . It iterates over elements in a list, and for each element, iteratively compares it to its predecessors and inserts it into its correct position among them.

compile with g++ --std=c++17 -Wall -o <output> <inputfile>.cpp

MERGE SORT

if the size of the List is at least 2  
  split the List into the left half and the right half  
  recursively sort left  
  recursively sort right  
  merge left and right into one List  
end if

mergeSort ( list ) {
if ( list.size > 1 ) {
split( list, left, right );
mergeSort( left );
mergeSort( right );
merge( left, right, list );
}
}

split ( list, left, right ) {
for each item in the left half of list (less than or equal to middle index)
add the item to left
for each item in the right half of list (greater than middle index)
add the item to right
}

merge( left, right, list ) {
while both left and right have more items
if the left item is less than the right item
add the left item to list
else
add the right item to list
while left has more items
add the left item to list
while right has more items
add the right item to list
}

QUICK SORT
Begin with an array arr.

Pick a pivot index. ~~Often at the end of the array.~~ or find using a median of three algorithm
Declare two indices j and i; and a temporary variable temp
- j is at the start of the array
- i is one less than the beginning of the array
Do while j < pivot:
1. If arr[j] < arr[pivot]:
  - i++
  - swap arr[i] and arr[j] using temp variable
    - assign temp = arr[i]
    - assign arr[i] = arr[j]
    - assign arr[j] = temp
2. j++
Now j = i. So i++.
Swap arr[i] and arr[j]. Set pivot = i.
- Now the arr[pivot] is in the right spot. i.e. all items left of pivot are less than the pivot and all items greater than the pivot are greater than the pivot.
Finally, recursively return quicksort(arr[:pivot - 1]) + [arr[pivot]] + quicksort(arr[pivot + 1:])

SELECTION SORT

Find the smallest value in the unsorted portion
Swap the value to the index after the end of the sorted portion
Repeat until the unsorted portion is empty

Worst case: $O (n^{2})$

Each pass of the array is $O (n)$
Up to $n$ passes required to sort the list